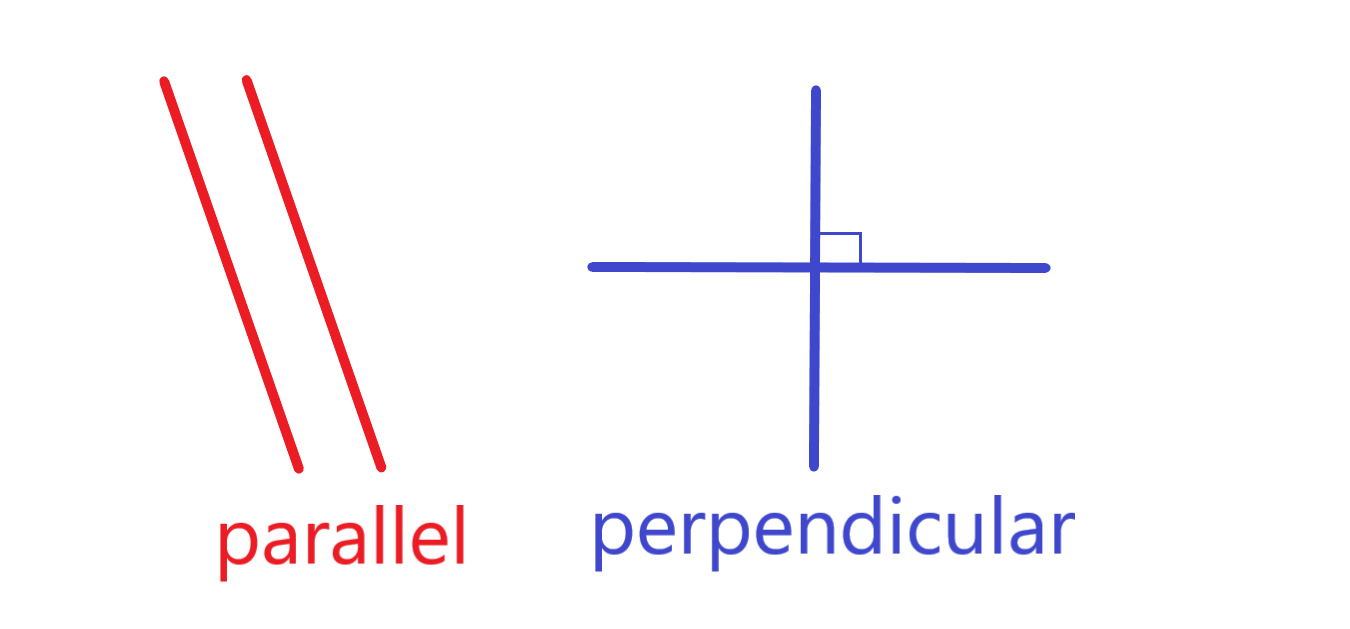
Teaching two similar concepts and their vocabulary terms at the same time creates confusion.
The classic example is teaching parallel and perpendicular on the same day. The two concepts have to do with orientation of lines and the new vocabulary terms for them are similar. So teaching them at the same time means some or many students will have the two terms confused for a long time. That is known as a chronic confusion–possibly permanent. They will know that orientation of lines is one of those two terms, possibly, but will be confused about which is which. The predictable conversation with the teacher goes thusly:
Teacher: See these two lines lines. Are they parallel or perpendicular?
Student: I think they’re perpendicular.
Teacher: Well…
Student: No, wait! I know. They’re parallel.
Teacher: Yes, you’re right. I’m glad you’ve learned that.
In case you missed it, the above student did NOT know the correct term. The student just knew it was one of two terms, but unsure as to which one. So the student picked one and as soon as there wasn’t confirmation by the teacher, switched to the other term. When you’re busy teaching it is easy to get fooled by that kind of response into assuming the students really did learn it.
Other examples abound in math. Teaching numerator and denominator in the same lesson is common. Teaching the terms proper fractions and improper fractions on the same day is another example. Acute and obtuse angles are yet another pair of chronically confused concepts that are introduced simultaneously.
Math teaching strategies: Separate the introduction of similar concepts in time.
If you teach one concept and only one of the pair, there’s no cause for confusion. It will still take a lot of repetition and practice for it to be cemented into memory, but students will be clear. If they use the term, for example parallel a lot of times in conjunction with examples they will soon (in a couple of weeks) be able to recall. However, you should pair the concept with non-examples of the concept. Not the opposite necessarily but just not an example of the concept.
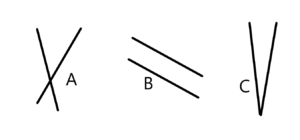
For example: For the picture to the right you would ask the students.
A “Are the two lines in item A parallel or not parallel?” Ans: Not parallel.
B “Are the two lines in item B parallel or not parallel?” Ans: Parallel.
C “Are the two lines in item C parallel or not parallel?” Ans: Not parallel.
Then after a couple of weeks you could introduce perpendicular. Again teach it on its own and then contrasted with non-examples until the vocabulary was clear. Probably for a couple of weeks. Only then can you combine both terms in the same lesson.
Another advantage of this approach is that you have avoided the other common mistake. Students sometimes come to the conclusion that all pairs of lines are either parallel or perpendicular. This method of introducing the concepts helps them realize that there are non-examples of each concept, parallel lines and ones that aren’t as well as perpendicular lines and ones that aren’t as well.