These effective math teaching strategies will help your students be more successful in learning math in your classroom. These are not the “cool, pedagogically-correct things” you can brag about in the teacher’s lounge or your master’s program classes, but they will improve math for the kids.
1. Help Students Memorize Math Facts
Once students know how to count out or figure out math facts, they are ready to begin memorizing the facts. After they memorize math facts, students can do math assignments quickly and learn math easily. It’s cruel to make them continue to figure out facts over and over again for months or years. Find and use a systematic method of memorizing math facts, so they have this tool at hand. There’s no magic bullet. Whatever you use needs to be systematic because it has to build gradually as students learn more and more of the facts. Any fact is easy to learn, but there are a lot of them, so that takes time.
Helping your students memorize math facts is like buying math power tools for them. It makes everything go quicker and much better. More gets done. Attitudes will improve. You don’t have to use Rocket Math, but you should use something! You will change their trajectory in and attitude about math for years to come. Learn more about why memorization is one of the essential math teaching strategies.
2. Ensure Math Facts are Mastered Before Starting Computation
Kids love to go fast. They hate the drudgery of having to count out facts or look multiplication facts up in a table. Once they know facts instantly, they can rip through math computation–and enjoy math because they love to go fast.
Not knowing math facts interferes with learning computation.
Here’s another surprise. Memorizing math facts makes learning multi-digit computation easier. Students who’ve memorized math facts are not distracted by having to stop and figure out what is 14 minus 9. They know it, without having to stop and think about it. They can give more of their attention to the details of the computation process and learn them better and easier than before. Try getting all your students fluent on the operation and then teach computation AFTER they have acquired fluency. You will be astonished at how quickly they learn. Read more about how math fact memorization supports computation.
3. Teach Computation Procedures With Consistent Language
Learning the procedures to do computational math processes is just like learning to follow a recipe. Eventually, you learn the key ingredients and can do it without looking and can do variations. But in the beginning, you need the written recipe to follow. You also need to do it the same way a few times to learn it. Winging it and teaching math “improv style” will only frustrate students.
Use a script or a process chart to keep the instructions consistent.
No one can remember exactly the way you said it yesterday or last week, which is why you need a script or a process chart on the wall so you can show the students that you are doing it the same way as last time. Repetition helps, but only if you’re repeating the same steps in the same order with the same wording.
Students will become flexible in their understanding at their own rate and in their own time. You just keep being consistent, and eventually, all the students will have mastered the procedure. I know that “thinking flexibly” is very much in fashion, but your students will thank you for providing them mastery of this one method of solving this type of problem. Flexibility can come later. Read more about how consistent language is key to teaching computation procedures.
4. Teach One Method and Only One Method at a Time
To solve a given type of problem, do NOT follow the advice to teach multiple solutions at one time. Teach only one way to go at a time, until that is learned, before introducing variations. Multiple solution paths will confuse all but the most advanced students in your room. Just teach them one procedure that will work every time with that type of problem. Your students will thank you for it.
It’s far better to know only one way to get there than to get lost every time!
Learning math procedures is no different than learning how to get to someone’s house (before GPS). You want to go the same way every time, until you have learned it. If you go a different way every time you’ll just be confused. You can learn another way later, once you can get there reliably using one route, but before that, you cannot learn another route, because you’ll mix up steps from each route. Read more about why teaching one procedure at a time is one of the effective math teaching strategies.
5. Separate the Introduction of Similar Concepts
The classic example is teaching parallel and perpendicular on the same day. The two concepts have to do with the orientation of lines, and the new vocabulary terms for them are similar. So teaching them at the same time means some or many students will have the two terms confused for a long time. That is known as a chronic confusion–possibly permanent. They will know that the orientation of lines is one of those two terms, but will be confused about which is which.
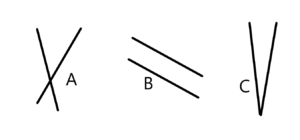
Parallel vs. Perpendicular
For example: For this picture, you would ask the students.
A “Are the two lines in item A parallel or not parallel?” Ans: Not parallel.
B “Are the two lines in item B parallel or not parallel?” Ans: Parallel.
C “Are the two lines in item C parallel or not parallel?” Ans: Not parallel.
After a couple of weeks of this kind of practice, you could introduce perpendicular. Again teach it on its own and then contrast perpendicularly with non-examples until the vocabulary is clear.
Probably do that for a couple of weeks. Only then can you combine both terms in the same lesson.
Numerator vs. Denominators
Other examples abound in math. Teaching numerator and denominator in the same lesson is common. Teaching the terms proper fractions and improper fractions on the same day is another example. Acute and obtuse angles are yet another pair of chronically confusing concepts that are introduced simultaneously. Separate them in time, and you’ll be amazed at how much better students can learn these concepts. Learn more about how to successfully teach similar concepts separately.
6. Teach New Concepts Using Common Sense Names
Here’s an example of the problem. A brachistochrone (pictured here) is a curve between two points along which a body can move under gravity in a shorter time than for any other curve. Introducing this concept and the term brachistochrone at the same time would cause students difficulty learning it.
When Instruction is not working
If you watch instruction where the term and the concept have been taught simultaneously, confusion ensues when the teacher uses the term. Sometimes the teacher will notice students looking confused and give a thumbnail definition or example of the term, and the students will then remember. However, the teacher should then realize that the concept was not connected to the new vocabulary term.
Students can quickly understand and use new concepts and ideas in math if they don’t have to learn a new word for it. Using a common sense term, the idea or concept can be applied to real-world problems almost immediately. Students can later quite easily learn proper vocabulary terms for concepts they understand and recognize. Here’s an example.
The “shortest time curve.”
I would call a brachistochrone the “shortest time curve.”** Instruction would proceed with the, “Do you remember that ‘shortest time curve’ we talked about last week?” Students would easily be able to remember it. Instruction would go like this: “So ‘the shortest time curve’ has some other cool properties. What’s the primary thing we know about the ‘shortest time curve’?” Students would easily be able to answer this question.
Then after students have worked with the concept of “the shortest time curve” for a couple of weeks, you can add the vocabulary term to it. “By the way, the proper mathematical name for “the shortest time curve” is called a brachistochrone. Isn’t that cool?” Read more on how to teach new math concepts with common sense names.
**Actually, that’s what brachistochrone means in Greek: brakhistos, meaning shortest and khronos meaning time.
Learn More Effective Math Teaching Strategies with Rocket Math
Rocket Math Online Game and Rocket Math Worksheets Program are math teaching strategies that will work for any classroom. Use the Pre-Test worksheets to understand how fast your students can answer math facts and what level they are at. The Rocket Math Online Game will help students succeed in math by creating a fun and enjoyable way for them to learn.