High-stakes state tests do not directly test fluency on math facts, although they should. Your students can become bogged down in deriving basic facts during state testing. When that happens they will be unable to demonstrate the higher-level math skills they have been learning. You may have a math fact fluency problem, depressing your math achievement scores, but not even know it. Here are six things to look for–to evaluate for yourself.
1) Finger counting during math testing shows a fact fluency problem
Students who are counting on their fingers (see above) during math testing are a definitive sign of a math fact fluency problem. Finger counting is a bad sign in grades 3 and above, where they should have mastered math facts. Students who don’t know the facts, need to use crutches to derive the answers to math facts. Crutches make doing simple calculations take a long time to complete anything. Your students may perform poorly on state tests just because they won’t complete the test for lack of time.
2) Students who lack math fact fluency need times tables available
When students in grades 3 or 4 and up have to do multiplication, they either have to know their facts or have a crutch. If you see times tables on student desks that shows that the students need these crutches, and therefore do not know the basic multiplication facts. Student folders sometimes come with these on the inside. Some teachers put up a large poster of the multiplication facts–even though students find it nearly impossible to use from their seats. Others provide laminated cards to the students which appear suddenly when students are set to do their “math work.” When you see those times tables being used by more than a couple of students during math, you can tell you have a fluency problem.
3) Students who lack math fact fluency don’t participate in math lessons
Good teachers work to engage the class. One good way, while working a problem for the class, is to ask the class for the answers to math facts. Watching a lesson you may be able to spot a class that lacks fact fluency. For example, imagine you watch the teacher demonstrating this problem.
Class, we begin this problem by multiplying nine times four. What’s nine times four, everybody?” [Only a couple of students answer.] Yes, 36. Now we write down the six and carry the 3 tens up to the tens place. Next, we multiply nine times six. What’s nine times six, everybody?” [After a long silence, one student answers.] Yes, 54. And we add the three to the 54, what do we get? [Several students call out the answer.] Yes, 57. That’s what we write down.
That interchange tells you there’s a math facts problem in this class. When the problem is very easy, like 54+3 you get a good response. When the fact is a “hard” one, you get silence and then one student answering. Medium facts get minimal response. This is a class that does not know their math facts.
4) Over-reliance on calculators signals a lack of math fact fluency
There are two kinds of over-reliance on calculators you may see in classrooms. In the first kind, you see students who do not know facts using calculators to tell them the answer to single-digit facts they should have memorized. Using calculators for single-digit facts is terribly slow and inefficient–and not what they are designed to do. You can see this over-reliance on calculators when observing in a classroom.
The second kind of problem is harder to spot. Using calculators without knowing math facts instantly can be dangerous. It is easy to make a data entry error, AKA a typo. When a user does that, they’re assumed to know math facts well enough to know when the answer is wrong, as in the example pictured here. A student who doesn’t know that 5 times 8 is 40 and therefore knows that 521 times 8 has to be more than 4,000 will accept the answer displayed on the calculator. Accepting incorrect answers from the calculator is a sign that students do not have an adequate mastery of facts.
5) Avoidance behaviors in math signal a lack of math fact fluency
Having to count out facts or look each fact up in a table is very slow and onerous. Students come to hate slogging through math computation that is so hard for them. Conversely, students who know facts instantly, hop right into assignments to get them done. Students like going fast doing math problems, just like they run for the joy of it on the playground. How do you know there is a fluency problem in the classroom? Students who lack fluency start avoiding getting started on computation work by getting water or sharpening pencils or just taking a break first.
6) Really slow computation during math lessons is due to a lack of math fact fluency
Good math teachers assign, within their lessons, a few math computation problems to do independently and then be checked as a group. If students know math facts they can do a few problems in a minute or two. Students who do not know math facts may take ten minutes or more to do the same mini-assignment. Students who are done and waiting with nothing to do, begin talking and distracting the others. When there’s that big of a discrepancy between the first and the last student to do a few problems, there is a fact fluency problem in the class.
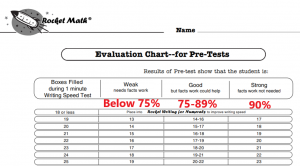
To be sure–give school-wide 1-minute tests of math fact fluency
If you see hints that your school may have a math fact fluency problem, it isn’t hard to know for sure. It only takes a couple of minutes. You can have everyone in the school take written 1-minute tests of math facts pretty easily. However, you’ll also need to evaluate how fast students can write. Students can’t answer math fact problems any faster than they write. You cannot expect a student who can write only 25 answers in a minute to answer 40 problems in a minute. Conversely, a student who can write 40 answers in a minute is not fluent with math facts if he answers only 30 problems in a minute.
You need a test of writing speed as well as a chart to evaluate their performance and the tests for the four main operations of addition, subtraction, multiplication, and division. Print these out for free at this link. But basically, a student who cannot answer math facts at 75% of the rate at which they can write, needs intervention.
Learn more about teaching math fact fluency
Teaching math fact fluency is necessary, of course, for fluent computation. Math fact fluency is also required for understanding and manipulating fractions. Find out more ways of successfully teaching math fact fluency to your students and why this skill is essential.
If you would like the free use of use the Rocket Math Online Game to assess for fluency, please contact Dr. Don at don@rocketmath.com.
