Dr. Don's Blog

List of Learning Tracks Continue to purchase

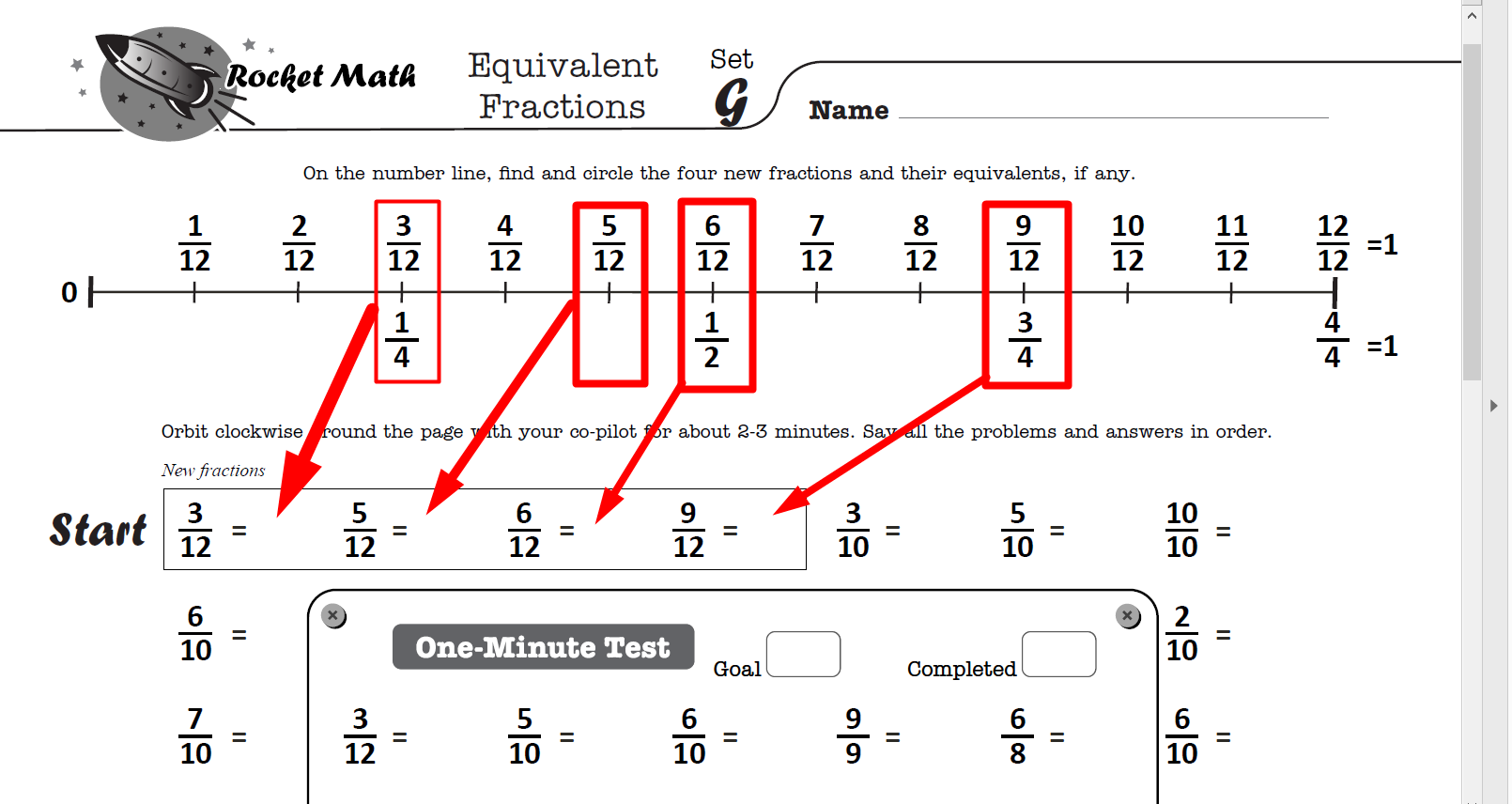
What do students learn?

 

List of Learning Tracks Continue to purchase

 

Mixed Integers combines Adding Integers and Subtracting Integers

If this mixed set goes too fast or is confusing for your students, an alternative is to start students with the two Learning Tracks that teach addition and subtraction separately.  The four addition processes are taught separately in the Learning to Add Integers Learning Track.   The four subtraction processes are taught separately in the Learning to Subtract Integers Learning Track.  If students have done those two Learning Tracks first, this will be a review and will be easier.

Mixed Integers teaches eight processes and two rules.

Mixed Integers displays problems on a vertical number line and then teaches students two rules about how to solve problems that add or subtract positive and negative numbers.
Rule 1:  When you add a positive number OR subtract a negative number, go UP.
Rule 2:  When you subtract a positive number OR add a negative number, go DOWN.

Students learn how these rules play out when starting with a positive number and a negative number, gradually learning these two variations of all four types of problems.  They learn to solve a problem type using the number line and then to recognize the pattern of each problem type by working several examples of each type.  This practice gives them a chance to build fluency with each problem type as they work with their partner on the top half of the page.  You will probably not be surprised that there is a one-minute test on each set.  The goals are slightly different than before.  Students are to be 100% accurate and to meet or beat their goal from the special writing speed test for mixed integers.

Video lessons teach the 8 processes.

There are 8 types of mixed integers problems (see below), between positive and negative numbers and the two operations. 8 online lessons teach students how each type of problem is solved and why it is correct.  (1) Mixed Integers Set A1 Positive add a positive

(2) Mixed Integers Set A2 Positive subtract a positive

(3) Mixed Integers Set D Negative add a positive

(4) Mixed Integers Set G Negative subtract a positive

(5) Mixed Integers Set J Negative subtract a negative

(6) Mixed Integers Set M Positive subtract a negative

(7) Mixed Integers Set P Positive add a negative

(8) Mixed Integers Set S Negative add a negative

 

List of Learning Tracks Continue to purchase

How does this Learning Track teach?

Learning to Subtract Integers displays problems on a vertical number line and then teaches students two rules about how to solve problems in which you subtract positive and negative numbers.

Rule 1:  When you subtract a positive number, go DOWN.
Rule 2:  When you subtract a negative number, go UP.

Doing problems on the vertical number line is more intuitively appealing because UP is more and DOWN is always less.  This makes crossing zero a little easier to comprehend.

Total of four problem types to learn.

Students learn how these two rules play out with two types of problems: when starting with a positive number and when starting with a negative number. Students gradually learn all four types of problems.  On each worksheet they see how to solve each problem type using the number line working with their partner.  Then students learn to recognize the pattern of each problem type by orally answering several examples of each type with their partner (going around the outside of the page).  You will probably not be surprised that there is a one-minute test on each set.   Students are to be 100% accurate and to meet or beat their goal from the special writing speed test for Learning to Subtract integers (the fastest goal is only 28 problems in a minute).

Online Video lessons can teach students the process.

Here are links to the 4 online lessons teach students how each type of problem is solved and why it is correct. These are available in the virtual filing cabinet as well.

(1) Subtract Integers Set A Positive subtract a positive

(2) Subtract Integers Set B Positive subtract a negative

(3) Subtract Integers Set G Negative subtract a negative

(4) Subtract Integers Set L Negative subtract a positive

 

List of Learning Tracks Continue to purchase

What is Skip Counting?

Not counting while skipping!  Learning to skip count by fours is to learn this sequence by memory: “Four, 8, 12, 16, 20, 24, 28, 32, 36, 40.” Skip counting is also known as learning the “count-by” series.

Why teach skip counting?

Skip counting is the best way for students to prepare for multiplication. It teaches the concept of successive addition which is the root of multiplication.  In addition, skip counting helps prepare the ground for memorizing the multiplication facts.  Students who have learned to skip count find the chore of memorizing multiplication facts much easier. This Learning Track is excellent for second or third grade students after learning addition and subtraction facts and before learning Multiplication facts. Skip counting is not something older students past fourth grade really need to do, and of course, it’s no longer useful once multiplication facts have been committed to memory.

Each series is broken into easy-to-learn parts

Students learn part of each sequence on a page, then the next page they learn the rest. For example: in Set O students learn to count by 3s to 12, (3, 6, 9, 12) then in Set P they learn to count by 3s to 21 (3, 6, 9, 12, 15, 18, 21), and then in Set Q they learn to count by 3s to 30 (3, 6, 9, 12, 15, 18, 21, 24, 27, 30).

How does Skip Counting teach?

As in most Worksheet program Learning Tracks, students practice with a partner who has the answers. Because of the way the rockets go around the page (see above), students and their checkers will have to pick up the pages and turn them as they are working. You’ll be able to see if they are really engaged and they will have fun turning the page around. The test in the center has them write the count-by series they have learned for one-minute and they need to meet or beat their best–just like the rest of Rocket Math. Here is the sequence students will learn in this order: 2s, 5s, 10s, 9s, 4s, 25s (so they can count quarters), 3s, 8s, 7s, and 6s. Probably our most fun Learning Track.

List of Learning Tracks Continue to purchase

What does this Learning Track teach?

Learning to Add Integers teaches four types of problems to solve.  It displays problems on a vertical number line and then teaches students two rules about how to solve problems that add positive and negative numbers.
Rule 1:  When you add a positive number, go UP.
Rule 2:  When you add a negative number, go DOWN.

Doing problems on the vertical number line is more intuitively appealing because UP is more and DOWN is always less.  This makes crossing zero a little easier to comprehend.

Students learn how these two rules play out with two types of problems: when starting with a positive number and when starting with a negative number. Students gradually learn all four types of problems.  On each worksheet they see how to solve each problem type using the number line working with their partner.  Then students learn to recognize the pattern of each problem type by orally answering several examples of each type with their partner (going around the outside of the page).  You will probably not be surprised that there is a one-minute test on each set.   Students are to be 100% accurate and to meet or beat their goal from the special writing speed test for Learning to Add integers (the fastest goal is only 28 problems in a minute).

Video Lessons for students to learn the process.

4 online lessons teach students how each type of problem is solved and why it is correct.

(1) Add Integers Set A Positive add a positive

(2) Add Integers Set B Positive add a negative

(3) Add Integers Set G Negative add a negative

(4) Add Integers Set L Negative add a positive

List of Learning Tracks Continue to purchase

Add and Subtract Fact Families are a different way to learn facts.

A number of math programs around the country introduce math facts in families.  Now Rocket Math does too!  A fact family includes both addition and subtraction facts. This program is Part 2 of Fact Families, coming after Fact Families 1 to 10. You can see above the 18 examples of fact families taught in this program starting with Set A; 11-2, 11-9, 9+2, & 2+9.  The sheet above shows the sequence of learning facts in the new Rocket Math  program Add-Subtract Fact Families from 11 to 18.  Each set that students learn from A to R adds just one fact family to be learned, so it isn’t too hard to remember.  (That’s the Rocket Math secret ingredient!) 

Learning math facts in families, is gaining in popularity these days.  Logic suggests that this would be an easier way to learn.  However, the research is not definitive that this is easier or a faster way to learn facts than separating the operations and learning all addition facts first and then learning all subtraction facts.  But learning in fact families is a viable option, and I wanted to have it available for Rocket Math customers.

Fact Families from 11 to 18 is part two and fit for second grade.

These facts come after the Add and Subtract Fact Families 10, which should be learned in first grade, so these are best for second grade.  The 25 fact families in 1s through 10s facts are just enough for one Rocket Math program.  It is a good and sufficient accomplishment for first grade.  With the 11 to 18 part for second grade there will be a lot of review.  In fact sets S through Z are all review. I have heard that some first grades prefer to keep the numbers small but to learn both addition and subtraction–so this program accomplishes that.

We  most sincerely want students to be successful and to enjoy (as much as possible) the necessary chore of learning math facts to automaticity. Please give us feedback when you use this program, Add-Subtract Fact Families 11 to 18,  letting us know how it goes for the students.

 

 

List of Learning Tracks Continue to purchase

A number of math programs around the country introduce math facts in families.  Now Rocket Math does too!  A fact family includes both addition and subtraction facts. You can see below the 25 examples of fact families taught in this program starting with Set A; 3+1, 1+3, 4-1 & 4-3.  The sheet shows the sequence of learning facts in the new Rocket Math  program Add-Subtract Fact Families to 10.  Each set that students learn from A to Y adds just one fact family to be learned, so it isn’t too hard to remember.  (That’s the Rocket Math secret ingredient!) 

Learning math facts in families, is gaining in popularity these days.  Logic suggests that this would be an easier way to learn.  However, the research is not definitive that this is easier or a faster way to learn facts than separating the operations and learning all addition facts first and then learning all subtraction facts.  But learning in fact families is a viable option, and we wanted to have it available for Rocket Math customers.

Flash news!! Someone looking for a master’s or doctoral thesis could do a comparative study of students using the fact families vs. the separated facts in Rocket Math. This could easily be a gold standard research study because you could randomly assign students to conditions within classrooms–the routine is the same for both–just the materials in their hands is different!  Just sayin’…

Best fit for first grade.  Dr. Don separated out the facts to 10 from the 11s-18s, because these 25 families are just enough for one Rocket Math program.  It is a good and sufficient accomplishment for first grade.  Some first grades prefer to keep the numbers small but to learn both addition and subtraction–so this program accomplishes that.

Add-Subtract Fact Families to 10 is the first half.  The rest of the addition and subtraction fact families, which students could learn in 2nd grade, are the Add-Subtract Fact Families 11 to 18.  We most sincerely want students to be successful and to enjoy (as much as possible) the necessary chore of learning math facts to automaticity.

List of Learning Tracks Continue to purchase

Why commit to memory equivalent fractions?

We expect students to reduce their answers to the lowest terms, but how can they if they don’t recognize them?  To do this easily, students need to know that six-eighths is equivalent to three-fourths and that four-twelfths is equivalent to one-third.  While they can calculate these, it is very helpful to know the most common equivalent fractions by memory.  Not knowing these by memory accounts for the most common problem students have in fractions: failing to “reduce their answers to simplest form.”

Each set (A through Z) has four fractions which are displayed on a fraction number line.  In addition to pairs of equivalent fractions, students frequently learn fractions equivalent to one, such as ten-tenths.  They also memorize fractions that can’t be reduced, for example three-fourths is only equivalent to three-fourths. Students use a number line and identify equivalent fractions by circling an equivalent pair of fractions.  They understand why they are equivalent as well as memorizing the pair.

Equivalent fractions, Factors, and Integers, are all pre-algebra programs that are recommended for upper elementary and middle school students who already know the basic facts.

5-minute Equivalent Fractions video lesson.

Dr. Don explains How the Equivalent Fractions program works.

Students will commit to memory 100 common equivalent fractions.

Click here for the full sequence of equivalent fractions that students will learn in this program.