Why use Rocket Math?

Two students participating in one of Rocket Math's math fluency programs

How School Math Fluency Programs Work

Posted on by Dr. Don

Math Fluency Programs should be part of on-going elementary school routines

Most elementary teachers do some activities to promote math fluency.  Yet many elementary children are not fluent with math facts by the time they hit upper elementary or middle school.  A hit-or-miss approach allows too many students, especially the most vulnerable, to slip through the cracks.   Math fluency programs, like Rocket Math’s Worksheet Program, need to be part of your elementary school’s routine.  Effective math fluency programs should be properly structured and every math teacher should be on board, every year.

Math fact fluency enables students to develop number sense

Many teachers learn in their training programs about the importance of “number sense.”  Students who have “number sense” can easily and flexibly understand relations between numbers.  They can recombine numbers in various ways and see the components of numbers.  Students with number sense can intuit the fact that addition and subtraction are different ways of looking at the same relations.

What is not taught in most schools of education is that developing fluency with the basic math facts ENABLES the development of number sense much better than anything else.  Once students memorize facts, they are available for students to call upon to understand alternate configurations of numbers. Students find it much easier to see the various combinations when they when they can easily recall math facts.  Once students master the basic facts, math games that give flexibility to thinking about numbers become much easier.

It may be hard for new teachers, straight from indoctrination in the schools of education, to imagine this is true.  However, if they land in an elementary school with a strong math fact fluency program they will see the beneficial effect of memorization.

young boy wearing a blue striped shirt counting to seven on his fingersWhy is math fact fluency important

In the primary grades, students who have not developed fluency in math facts will have a harder time learning basic computation.

Students who are not fluent with math facts find the worksheets in the primary grades to be laborious work.  They finish fewer of them and may begin to dislike math for this reason.

By the time students reach upper elementary, if they have not memorized the math facts, they find it very difficult to complete math assignments at their grade level.  They find themselves unable to estimate or do mental math for problem-solving.  The need to figure out math facts will continue to distract non-fluent students while they are learning new math procedures like algorithms.

In the upper grades, their inability to figure out multiplication facts becomes a huge stumbling block.  Manipulations of fractions, decimals, and percentages will not make intuitive sense to students because they haven’t memorized those facts.  Without math fact fluency, students rarely succeed in pre-algebra and may be prevented from learning algebra and college-level math entirely.

Math fact fluency must be assured through regular monitoring

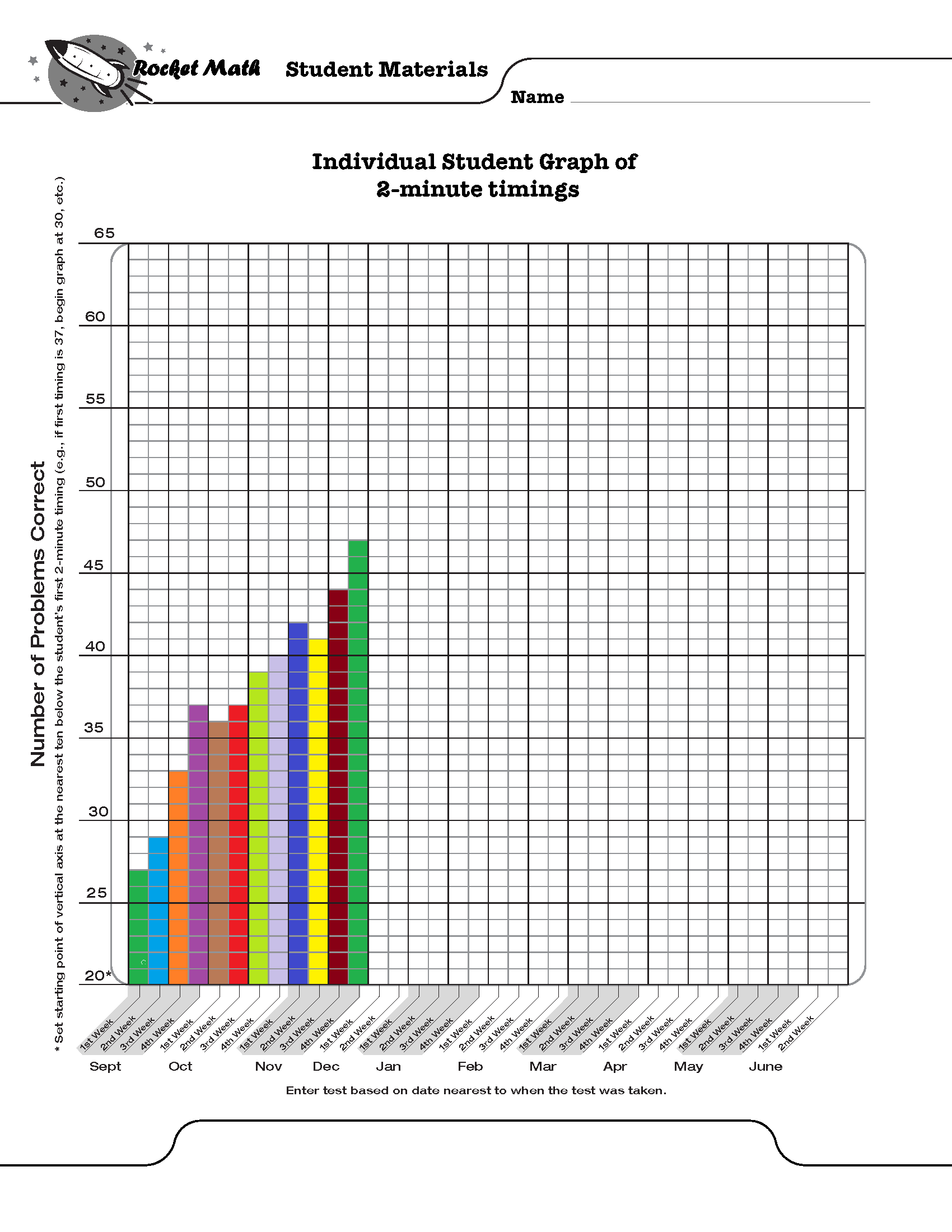Some students will need up to ten times more practice to develop math fluency than other students.  Therefore, monitoring student success in memorizing the facts is critical. Teachers can assume that what is “enough practice” for some students is NOT going to be enough practice for all students.  Effective math fluency programs must have a progress monitoring component built in.  Progress monitoring gives comparable timed tests of all the facts at intervals during the year.  Teachers look at the results of these timed tests to check on two things:

1. Are students gradually improving their fluency with all the facts gradually over the year? 

In other words, are students able to answer more facts in the same amount of time?  If they aren’t improving, then the instructional procedures aren’t working and need to be modified or replaced.  Math fluency programs like Rocket Math’s Worksheet Program have two minute timings of all the facts in each operation that can be given and the results graphed to see if there is steady improvement.

2. Are all students reaching expected levels of performance at each grade level each year?

Proper math fluency programs identify students who are not meeting expectations and give them more intensive interventions.  Ultimately, by the end of fourth grade all students should be able to fluently answer basic 1s – 9s fact problems from memory in the four operations of add, subtract, multiply and divide. Fluent performance is generally assumed to be 40 problems per minute, unless students cannot write that quickly.

Expectations vary by grade level and the sequence with which schools teach facts can vary.  While it is great to achieve all that the Common Core suggests, it is critical only to assure that students master and gain fluency in 1s through 9s facts.  Some schools in some neighborhoods may find that waiting until second grade to begin math facts may not provide enough time for all students to achieve fluency.  When to begin fact fluency and how much to expect each year should be based on experience rather than some outside dictates.

Successful math fluency programs must have these 3 features

 

  1. Sequences of small sets

    No one can memorize ten similar things, like the 2s facts, all at once. Students easily master math facts when they can learn and memorize small amounts of facts at one time. Effective math fluency programs define math fact sequences, which students memorize at their pace before moving onto new math facts. Rocket Math’s fluency program uses only two facts and their reverses in each set from A through Z.

  2. Self-paced progress

    Even if you only introduce small sets of math facts, some students need more time to memorize than others.  If you introduce the facts too fast, students will begin to jumble them together and progress will be lost. The pace of introducing facts must be based on mastery—not some pre-defined pace.  This is why doing all the multiplication facts as a class in the first six weeks of third grade does not work.  It is just too fast for some students.  Once they fall behind it all becomes a blur.

  3.  Effective practice and corrections

    When students are practicing facts, they will come to ones they have forgotten or can’t recall immediately.  Those are the facts on which they need more practice.  Allowing students to stop and figure out the facts they don’t know while practicing, does not help the student commit them to memory.  Instead, students need to IMMEDIATELY receive the fact and the answer, repeat it and try to remember it.  Then they need to attempt that fact again in a few seconds, after doing another couple of problems.  If they have remembered the fact and can recall it, then they are on their way to fluency.  But students must practice the next day to cement in that learning.

Math fluency programs like Rocket Math’s Worksheet Program teach students math facts in small sets, allow students to progress at their own pace, and support effective practice and error correction. Each Rocket Math Worksheet program has 26 (A to Z) worksheets specially designed to help kids gradually (and successfully) master math skills. Gain access to all of them with a Universal Subscription or just the four basics (add, subtract, multiply, divide–1s to 9s) with a Basic Subscription.

 

 

Math Teaching Strategy #1: Help students memorize math facts

Posted on by Dr. Don

Once students know the procedure, they should stop counting and memorize!

When it comes to math facts like 9 plus 7 or 8 times 6 there are only two things to know.  1) A procedure to figure it out, which shows that you understand the “concept.”  2) What’s the answer?

It is important for students to understand the concept and to have a reliable procedure to figure out the answer to a math fact.  But there is no need for them to be required to use the laborious counting process over and over and over again!  Really, if you think about it, even though this student is doing his math “work” he is not learning anything. 

Math teaching strategy:  Go ahead and memorize those facts.

(It won’t hurt them a bit.  They’ll like it actually.)

Once students know the procedure for figuring out a basic fact, then they should stop figuring it out and just memorize the answer.  Unlike capitals and countries in the world, math facts are never going to change.  Once you memorize that 9 plus 7 is 16, it’s good for a lifetime.  Memorizing math facts makes doing arithmetic MUCH easier and faster.  Hence our tagline

Rocket Math: Because going fast is more fun!

Memorizing facts is the lowest level of learning.  It’s as easy as it gets.  But memorizing ALL the facts, which are similar, is kind of a long slog.  Some kids just naturally absorb the facts and memorize them.

Math teaching strategy: Find a systematic way for students to memorize.

A lot of students don’t learn the facts and keep counting them out over and over again.  They just need a systematic way of learning the facts.  Students need to spend as much time as necessary on each small set of facts to get them fully mastered.  If the facts are introduced too fast, they start to get confused, and it all breaks down.  Each student should learn at their own pace and learn each set of facts until it is automatic–answered without hesitation and without having to think about it.  This can be accomplished by everyone, if practice is carefully and systematically set up.  It should be done, because the rest of math is either hard or easy depending on knowing those facts.  And don’t get me started about why equivalent fractions are hard!

 

Math Teaching Strategies #2: Ensure math facts are mastered before starting computation

Posted on by Dr. Don

Rocket Math can make learning math facts easy.  But even more important it can make teaching computation easy too!  One of the first teachers to field test Rocket Math was able to teach addition facts to her first grade class, and then loop with them into second grade, where she helped them master subtraction facts as well.  She told me that because her second graders were fluent with their subtraction facts, they were ALL able to master regrouping (or borrowing) in subtraction in three days.  What had previously been a three week long painful unit was over in less than a week.  All of them had it down, because all they had to think about was the rule for when to regroup.  None of them were distracted by trying to figure out subtraction facts.

Math teaching strategy: Get single-digit math facts memorized before trying to teach computation.

When math facts aren’t memorized, computation will hard to learn, hard to do, and full of errors.

When math facts aren’t memorized, computation will be hard to learn.   I used to think computation was intrinsically hard for children to learn.  Because it was certainly hard for all of my students with learning disabilities.  But none of them had memorized the basic math facts to the point where they could answer them instantly.  They always had to count on their fingers for math.

When I learned more about the process of learning, I found out that weak tool skills, such as not knowing math facts,  interferes with learning the algorithms of math.  When the teacher is explaining the process, the student who hasn’t memorized math facts is forced to stop listening to the instruction to figure out the fact.  When the student tunes back into instruction they’ve missed some essential steps.  Every step of computation involves recalling a math fact, and if every time the learner has to turn his/her attention to deriving the math fact they are constantly distracted.  That interferes with the learning process.

When math facts aren’t memorized, computation will be hard to do.   Having to stop in the middle of the process of a multi-digit computation problem to “figure out” a fact slows students down and distracts them from the process.  It is easy to lose your place, or forget a step when you are distracted by the difficulty of deriving a math fact or counting on your fingers.  It is hard to keep track of what you’re doing when you are constantly being distracted by those pesky math facts.  And of course, having to figure out facts slows everything down.

I once stood behind a student in a math class who was doing multiplication computation and when he hesitated I simply gave him the answer to the math fact (as if he actually knew them).  He loved it and he was done with the small set of problems in less than half the time of anyone else in his class.  Children hate going slow and slogging through computation. Conversely, when they know their facts to the level of automaticity (where the answers pop unbidden into their minds) they can go fast and they love it.  That’s why “Because going fast is more fun!” is the Rocket Math tag line.

When math facts aren’t memorized, computation will be full of errors.  When I learned more about basic learning, I found out that the frequent student errors in computation were not simply “careless errors.”  I thought they were because when I pointed out simple things like, “Look you carried the 3 in 63 instead of the 6.” my students would always go “Oh, yeah.” and immediately correct the error.  If I asked them they knew that they were supposed to carry the number in the tens column, but they didn’t.

I thought it was carelessness until I learned that such errors were the result of being distracted.  Not by the pretty girl next to you, but by having to figure out what 7 times 9 was in the first place.  After going through the long thinking process of figuring out it was 63 they were so distracted that they carried the wrong digit.  Not carelessness but distraction.  Once students instantly know math facts without having to think about it, they can pay full attention to the process.  They make far fewer errors.

In short, don’t be cruel.  If you have any autonomy available to you, first help your students memorize math facts and then teach them how to do computation in that operation.  In other words, teach subtraction facts before subtraction computation.  If you help them get to the point where math fact answers in the operation come to them without effort, you’ll be amazed at how much easier it is to teach computation, for them to do it and at the accuracy with which they work.

Rocket Math: Can students really learn this way? (It seems too easy.)

Posted on by Dr. Don

At first, it may seem like the way Rocket Math presents the same simple facts over and over, is so easy it must be a waste of time.

       But like anything you learn, you have to start where it seems easy and then build up to where it is hard.  Rocket Math has been effective helping students learn their math facts for over 20 years.  It is designed according to scientifically designed learning principles, which is why it works, if students will work it.  Rocket Math carefully and slowly introduces facts to learn in such a way that students can achieve fluency with each set of facts as they progress through the alphabet A through Z.  Let me explain.
         Set A begins with two facts and their reverses, e.g., 2+1, 1+2, 3+1 and 1+3.  Dead simple, huh?  But in answering those the student learns what it is like to instantly “know” an answer rather than having to figure it out.  The student says to himself or herself, “Well, I know that one.”  The student learns he or she can answer a fact instantly with no hesitation every time based on recall and not figuring it out.  The game requires the student to answer the problems at a fast rate, proving that he or she knows those facts.  Once that level is passed the game adds two more facts and their reverses,.  The same process of answering them (and still remembering Set A) instantly with no hesitation every time.  When that is achieved, the game moves the student on to Set C, two more facts and their reverses.  Eventually, every student gets to a fact on which they hesitate (maybe one they have to count on their fingers), meaning they can’t answer within the 3 seconds allowed.  Mission Control then says the problem and the correct answer, has the student answer that problem, then gives two different facts to answer and goes back to check on the fact the student hesitated on again.  If the student answers within 3 seconds then the game moves on.
 
     In the Take-Off phase the student is introduced to the two new facts and their reverses.  That’s all the student has to answer.  But the student has to answer each one instantly.  If the student is hesitant on any of those facts (or makes an error) then they have to Start Over and do the Take-Off phase over again.  They have to do 12 in a row without an error or a hesitation.  Once the Take-Off phase is passed the student goes into the Orbit phase, where there is a mix of recently introduced facts along with the new facts.  The student has to answer up to 30 facts, and is allowed only two errors or hesitations. After the third error or hesitation the student has to Start Over on the Orbit Phase.  Once the Orbit phase is passed, the student goes on to the Universe phase, which mixes up all the facts learned so far and presents them randomly.  Again the student has to do up to 30 problems and can only hesitate on 2 or them or he or she has to start over.  But once the student proves that all of those facts can be answered without hesitation, the game moves on to the next level, introducing two more facts and their reverses.
      In the Worksheet Program, students practice with a partner.  In the Online Game the student practices with the computer.  In both versions of Rocket Math the students follow the same careful sequence and slowly, but successfully build mastery of all of the facts in an operation.  It’s hard work and takes a while, but we try to make it fun along the way.  It will work for everybody, but not everybody is willing to do the work.  At least, now you understand how Rocket Math is designed so it can teach mastery of math facts.

What if teachers won’t do Rocket Math?

Posted on by Dr. Don

Don’t argue, just prove it works! 

Joyce asks: 

How can we encourage the teacher who refuses rocket math and administration does not reinforce (or enforce) the program’s use?

Dr. Don’s response:

  Joyce,

     This is a great question.  Frankly, one of the most annoying things I found during my time as a teacher were the constant “new” fads.  I got sick and tired of being told to do things I knew would not work.  I don’t blame people for being skeptical or an administration that won’t go to bat for a new curriculum.  I think it is the responsible thing to do. Which is why schools should test everything for themselves, which isn’t that hard to do.  Prove to yourself it works with your students in your school with your staff.  Then you know it is worth doing.  Only then do you have a responsibility to reinforce the program’s use, only after it is proven.
In one of the first schools to use Rocket Math we had a veteran teacher who said she did not think Rocket Math would be any better than the things she had been doing to help her students learn math facts for years.  The principal wisely allowed as how that might be possible, but asked if she would be willing to test her assertion.  Rocket Math has 2-minute timings of all the facts which the students take every couple of weeks.  The principal asked if she would give that test to her students at the beginning and the end of the year and compare her results with that of other classes.  She agreed.  At the end of year the Rocket Math students were far higher in their fluency than her students, even though at the beginning of the year her students had been more fluent than the other students.  At that point she said, “Well this proves it to me.  I’ll be using Rocket Math next year.”
   Just use those 2-minute timings as pre and post tests and see if there is anything that will beat Rocket Math.  Any teacher worth their salt should want to use a curriculum that is effective and helps students learn.
I have the following standing offer on my website.  If any school will conduct research comparing Rocket Math to some other method of practicing math facts and share your results–I will refund half of the purchase price of the curriculum.  If a school finds some other method is more effective, I will refund 100% of your purchase price.

Integers learning tracks are a part of Universal subscription

Posted on by Dr. Don

Using a vertical number line can help provide certainty.

Adding and subtracting positive and negative numbers can be confusing for students. You can either start with a positive or a negative number and combine it with a positive or a negative number. That makes for four types or patterns of problems. Then when you consider addition and subtraction, the total is 8 problem types. Rocket Math has three learning tracks to help students learn how to deal with integers. Mixed Integers include all eight types, whereas Learning to Add Integers and Learning to Subtract Integers each just deal with four types. [Mixed Integers may be too hard for some or all of your students–meaning they can’t pass levels in 6 tries. In that case, put them through the Learning to Add Integers and Learning to Subtract Integers first.]  

Part 1: Using the vertical number line to solve integers problems

The first issue for students is just to be certain of the answer. A vertical number line, where “up” is more and “down” is less helps provide certainty.

I have posted a series of free lessons online (links below) that use a vertical number line and a consistent procedure to take the confusion out of the process. Students can solve all eight types of problems with the same process on the vertical number line. Using the vertical number line there are two rules to learn. Rule 1: When you add a positive or subtract a negative, you go up on the number line. Rule 2: When you subtract a positive or add a negative, you go down on the number line.

So the first thing to figure out is what you are being asked to do (add or subtract a positive or a negative), and then use the rule to tell you whether you’re going up or down. Next step in the procedure is to circle the starting point on the number line. Once you circle the starting point, you show how far you’re being asked to go. You simply make the right number of “bumps” going either up or down from where you start. That gives you the answer without any uncertainty. These online lessons are quick (about 2 minutes) and identify a pattern of whether the answer is like the sum or the difference between the numbers. Once students can recognize the pattern they can begin to answer fluently and without a struggle

(1) Mixed Integers Set A1 Positive add a positive

(2) Mixed Integers Set A2 Positive subtract a positive

(3) Mixed Integers Set D Negative add a positive

(4) Mixed Integers Set G Negative subtract a positive

(5) Mixed Integers Set J Negative subtract a negative

(6) Mixed Integers Set M Positive subtract a negative

(7) Mixed Integers Set P Positive add a negative

(8) Mixed Integers Set S Negative add a negative

 

 

Part 2: Using the Rocket Math Integers learning track(s) to develop fluency in recognizing the type of problem

Here is a part of a page from the Mixed Integers learning track. The paired practice part of the program helps students learn to quickly and easily recognize each pattern.  First, students use the vertical number line to work on a problem. In this example: -6 minus (-4). Then they have a set of problems with the same pattern (a negative subtracting a negative), which they should be able to answer orally without using the number line. Each worksheet includes all the types learned so far in the learning track.

As with all Rocket Math programs, there is a 2 to 3-minute practice session (at this level, I’d recommend 3 minutes), with a partner. Then the two switch roles. The practice is followed by a one-minute test. If the student can answer the problems in the test fluently (essentially without hesitations), the level is passed. As always, the student’s goals are individually determined by a Writing Speed Test. If a given level is still difficult, the student stays with that level a bit longer.

When a new pattern or type of problem is first introduced the one-minute tests will have a whole row of problems that are the same pattern. When the student passes the level, the next test will have two types of problems in each row. The next level has 3 types in a row, culminating in the fifth level, where the problem types are mixed. This way, the student develops fluency in recognizing the type of problem and how to derive the answer quickly. The Learning to Add Integers and Learning to Subtract Integers learning tracks take more time to learn the patterns, while Mixed Integers move more quickly.

Don’t forget that Rocket Math has a money-back guarantee. So if this doesn’t work for you and your students, we will refund your subscription price.

 

Are your students wary of working with integers?

Posted on by Dr. Don

Many students find integers confusing.  If you add a negative to a negative are you getting more or less??? Over the years different “rules” have been used to try to remember what should happen.  Rules such as “two negatives make a plus” or “opposite signs subtract.”  Whatever is used to try to remember, it interferes with a student’s ability to quickly and reliably get the answers without having to stop and puzzle it out.

A screenshot of Rocket Math's beginning integers program where students learn through vertical graphs.A Vertical Number line is more intuitively obvious for learning integers.

I have posted a series of free lessons online (links below) that use a vertical number line to take some of the confusion out of the process.  Turns out there are a total of eight types of problems but all of them can be solved with the same process on the vertical number line.  Intuitively on a vertical number line, up is more and down is less.

(1) Mixed Integers Set A1 Positive add a positive

(2) Mixed Integers Set A2 Positive subtract a positive

(3) Mixed Integers Set D Negative add a positive

(4) Mixed Integers Set G Negative subtract a positive

(5) Mixed Integers Set J Negative subtract a negative

(6) Mixed Integers Set M Positive subtract a negative

(7) Mixed Integers Set P Positive add a negative

(8) Mixed Integers Set S Negative add a negative

 

Two rules to learn: when to go up and when to go down.

Using the vertical number line there are two rules to learn.  Rule 1: When you add a positive or subtract a negative you go up on the number line.  Rule 2: When you subtract a positive or add a negative you go down on the number line.

So the first thing to figure out is whether you’re going up or down.  Once you do that you simply make “bumps” going either up or down from where you start.  That gives you the answer without any uncertainty.  These lessons are quick (about 2 minutes) and identify a pattern of whether the answer is like the sum or the difference between the numbers.  Once students can recognize the pattern they can begin to answer fluently and without a struggle.

To help with the work of learning to quickly and easily recognize each pattern in Integers Rocket Math now includes three “Integers” Learning Tracks in our Worksheet Program Universal Level Subscription.    (Click here to get a 60-day initial trial subscription for less than the standard full-year subscription.)

Screen shot of Rocket Math's integers program list.

Learn adding and subtracting separately or mixed.

The first integers learning track, Learning to Add Integers, is limited to adding integers.  In the above list of lessons, the adding lessons are numbers 1, 3, 7, and 8.  The second integers learning track, Learning to Subtract Integers, is limited to subtracting integers and teaches the processes shown in lessons 2, 4, 5, and 6.  The third learning track, Mixed Integers Drawer combines all 8 processes into one learning track.  If students are likely to have issues or begin to find the Mixed Integers lessons difficult, have them do the separate operation first.

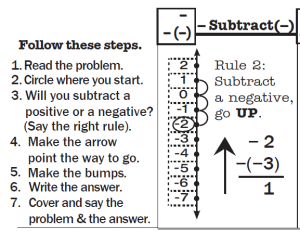In the Rocket Math Integers lessons, students use the vertical number line to work a problem. A screen shot of Rocket Math's subtracting integers worksheet.In this example: -2 minus (-3).  They use a rule and then apply it to the number line to find the answer. Then they have a set of problems with the same pattern they can orally answer without having to use the number line.

Students practice with a peer partner

As with all Rocket Math programs, there is a 3-minute practice session, with a partner.  The partner who is checking has the answer key and corrects all errors immediately.  Then the two switch roles.  Then the practice is followed by a one-minute test.  If the student can answer the problems without hesitation the level is passed.  If it is still difficult the student stays at that level a bit longer.  When a new pattern is introduced the tests will have a whole row of problems that are the same pattern. When that level is passed the next test will have two types of problems in each row.  The next level has 3 types, then 4 types in each row.  Then the problem types are mixed.  This way the student develops fluency in recognizing the type of problem and how to derive the answer quickly.

Rocket Math has a money-back satisfaction guarantee.  If you try this and find it isn’t everything you hoped, for in terms of helping your students become fluent with integers, I’ll gladly refund your money.  I’m betting they’re going to love it.

 

Foolproof method for finding factors

Posted on by Dr. Don

Knowing when you’ve found ALL the factors is the hard part.

Students have to learn how to find the factors of a number because several tasks in working with fractions require students to find the factors of numbers. Thinking of some of the factors of a number is not hard. What is hard is knowing when you have thought of ALL the factors. Here is a foolproof, systematic method I recommend: starting from 1 and working your way up the numbers. This is what student practice in the Worksheet Program Factors Learning Track.  Students also learn the pairs of factors in this sequence in the Online Game.

Dr Don has a white board type video lesson that explains this in 6 minutes.

https://www.educreations.com/lesson/view/how-to-find-all-the-factors-of-a-number/46790401/

Bookmark this link so you can show it to your students.

How to find all the factors of numbers
Always begin with 1 and the number itself-those are the first two factors. You write 1 x the number.  Then go on to 2. Write that under the 1. If the number you are finding factors for is an even number then 2 will be a factor. Think to yourself “2 times what equals the number we are factoring?” The answer will be the other factor.
However, if the number you are finding factors for is an odd number, then 2 will not be a factor and so you cross it out and go on to 3. Think to yourself “3 times what equals the number we are factoring?” There’s no easy rule for 3s like there is for 2s. But if you know the multiplication facts you will know if there is something. Then you go on to four—and so on.

The numbers on the left start at 1 and go up in value.  The numbers on the right go down in value.  You know you are done when you come to a number on the left that you already have on the right.  Let’s try an example.

Factors Answers d

Let’s find the factors of 18.  (To the left you see a part of a page from the Rocket Math factoring program.)
We start with the first two factors, 1 and 18. We know that one times any number equals itself. We write those down.
Next we go to 2. 18 is an even number, so we know that 2 is a factor. We say to ourselves, “2 times what number equals 18?” The answer is 9. Two times 9 is 18, so 2 and 9 are factors of 18.
Next we go to 3. We say to ourselves, “3 times what number equals 18?” The answer is 6. Three times 6 is 18, so 3 and 6 are factors of 18.
Next we go to 4. We say to ourselves, “4 times what number equals 18?” There isn’t a number. We know that 4 times 4 is 16 and 4 times 5 is 20, so we have skipped over 18. We cross out the 4 because it is not a factor of 18.
Next we go to 5. We might say to ourselves, “5 times what number equals 18?” But we know that 5 is not a factor of 18 because 18 does not end in 5 or 0 and only numbers that end in 5 and 0 have 5 as a factor. So we cross out the five.
We would next go to 6, but we don’t have to. If we look up here on the right side we see that 6 is already identified as a factor. So we have identified all the factors there are for 18. Any more factors that are higher we have already found. So we are done.

Now let’s do another number.  Let’s find the factors of 48. 

We start with the first two factors, 1 and 48.  We know that one times any number equals itself.

Next we go to 2.  48 is an even number, so we know that 2 is a factor.  We say to ourselves, “2 times what number equals 48?”  We might have to divide 2 into 48 to find the answer is 24.  But yes 2 and 24 are factors of 48.

Next we go to 3.  We say to ourselves, “3 times what number equals 48?”   The answer is 16.  We might have to divide 3 into 48 to find the answer is 16.  But yes 3 and 16 are factors of 48.

Next we go to 4.  We say to ourselves, “4 times what number equals 48?”  If we know our 12s facts we know that 4 times 12 is 48.  So 4 and 12 are factors of 48.

Next we go to 5.  We might say to ourselves, “5 times what number equals 48?”   But we know that 5 is not a factor of 48 because 48 does not end in 5 or 0 and only numbers that end in 5 and 0 have 5 as a factor. So we cross out the five.

Next we go to 6. We say to ourselves, “6 times what number equals 48?”  If we know our multiplication facts we know that 6 times 8 is 48.  So 6 and 8 are factors of 48.

Next we go to 7.   We say to ourselves, “7 times what number equals 48?”   There isn’t a number.  We know that 7 times 6 is 42 and 7 times 7 is 49, so we have skipped over 48.  We cross out the 7 because it is not a factor of 48.

We would next go to 8, but we don’t have to.  If we look up here on the right side we see that 8 is already identified as a factor.  So we have identified all the factors there are for 48.  Any more factors that are higher we have already found.  So we are done.

“Knowing” means never having to figure it out

Posted on by Dr. Don

Most people, for example, know their name, by memory.

In a previous blog I discussed  What does CCSS mean by “know from memory?”    

A reader asked the following question:

This topic of “know from memory” is something I have been digging into as a special educator. I wonder what your thoughts are about whether certain accommodations from these “know from memory” standards would actually be modifying the curriculum?

For example, if we used “extra time to respond” and the student had to use their fingers or some other method to count, would they then not be doing the standard?

This relates to where I’m at in middle school math, but I think that it’s reflected in the continuum of the common core maths.

Thanks.

Dr. Don’s response: 

Actually, your example is very clear that it is not “knowing from memory.” You are describing “deriving from a strategy” or what I call, “figuring it out.” When you know it from memory, when you recall the answer, then you stop having to “figure it out.”

Knowing from memory and figuring something out are two very different things. I used to ask workshop participants to imagine sitting next to me in a bar and asking me for my name. What if, instead of saying, “Hi, my name is Don,” something different happened?  What if, like the man pictured above, I was puzzled and said, “Wait a second, I have it here on my driver’s license.” Most people would likely turn their attention elsewhere while wondering what kind of traumatic brain injury I had sustained! They would very likely say to themselves, “OMG, that man doesn’t know his own name.”

The purpose of the verbal rehearsal that is a daily part of Rocket Math is to cement these basic facts in memory. Then when a student says to themselves, “8 times 7 is,” the answer pops into their mind with no effort. It takes quite a bit of practice to achieve that. However, the ability to instantly recall the answers to basic math facts makes doing mathematical computation a relative breeze. It make seeing relationships among numbers very obvious. It makes reducing fractions and finding common denominators easy. That’s why the Common Core thinks “knowing from memory” is so worthwhile. It’s why I began promoting Rocket Math in the first place.

Do you know the active ingredient in Rocket Math?

Posted on by Dr. Don

Timed tests are not the important part of Rocket Math.

The “active ingredient” in the Rocket Math prescription, the thing that makes it work, is not timed tests.  Timed tests don’t actually teach and often don’t really help students develop fluency.  The usual timed tests of a random selection of all the facts can assess fluency in math–but they don’t work to develop it!

The “active ingredient,” the thing that makes Rocket Math effective, is verbal rehearsal.  When students practice with their partner the students read the facts and RECALL the answers from memory and say them aloud.  That verbal rehearsal is what cements them into memory.  Reading the fact and recalling the answer from memory strengthens the neural connection.

Why do we give the daily tests in Rocket Math?  Not to teach, but only to assess whether the facts introduced thus far have been learned well enough for the student to have new facts added to what they are learning.  Individual students learn at different rates.  Some students need only a couple of days of practice to memorize two new facts while others may need several days.  The purpose of the daily tests is just to see if the student needs more practice time, or is ready to “swallow” some more facts.

As I note in my basic training presentation, “It’s like feeding mush to a baby.  You have to make sure they have swallowed the last mouthful before you give them more.”   See an explanation in this You Tube video in our Rocket Math channel: https://youtu.be/J8cWSDG0Di8